알파곰 (jaehc)

데이터과학에 관심있는 직장인 개발자입니다.

Affinity Propagation 살펴보기

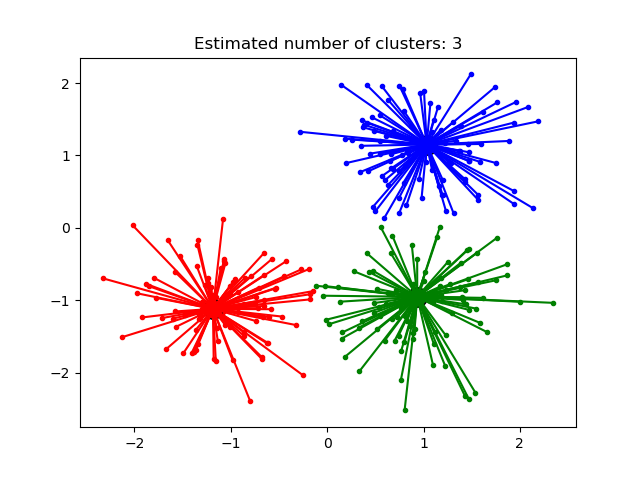
sphx_glr_plot_affinity_propagation_001

이번 글에서는 Affinity Propagation에 대해서 간략히 알아봅시다. ML에 관심 있는 분이라면 자주 접했을 데이터 사이언스 스쿨에도 관련한 소개 글이 있습니다. 실제로 많이 쓰이는 지는 잘 모르겠고, 저도 한 번도 써본 적은 없긴 하지만, 잊을만하면 문서에 가끔 나와서 매번 넘어가다가, 우연히 towards data science에 추천 글이 올라왔기에 키 아이디어를 위주로 정리하고 넘어가려고 합니다.

본문에 있는 그림과 내용은 하단의 References 섹션에 나열된 사이트들로부터 카피해온 것임을 밝힙니다. 본문 중간에도 필요하면 참고한 문서로의 링크를 추가했습니다.

Affinity Propagation

Affinity Propagation(이하 AP)은 비지도 클러스터링 기법의 하나입니다. 다시 말해서, 데이터에 대한 설명을 거의 듣지를 못해서, 진짜로 데이터 구조를 탐험부터 해야 하는 상황에서 사용하는 기법의 하나라고 할 수 있습니다. 굿럭!

k-means/k-medoids와 비교해서 이해하는 것이 좋은데 그 공통점과 차이점은 다음과 같습니다.

공통점

두 알고리즘 모두 클러스터 형태가 둥글어야 하는(globular) 가정이 있습니다.
k-means의 변형인 k-medoids와 동일하게 cluster center를 data point 자체(exemplar)를 사용합니다. 참고로 k-means는 클러스터에 속한 멤버의 평균값을 cluster center로 합니다.

차이점

AP는 k-means와 다르게 클러스터의 개수 k를 지정할 필요가 없습니다.
AP는 k-means와 다르게 클러스터들이 공간을 동일한 크기로 분할하는 것을 강요하지 않습니다. 참고: Visualizing the stock market structure

계산 복잡도는 $O(N^{2}T)$ 인데, 여기서 N은 샘플 수, T는 알고리즘 반복 횟수이다. 공간복잡도는 $O(N^{2})$이다. 복잡도가 높기 때문에 작은 데이터에만 사용할 수 있는 알고리즘입니다. [1]

Algorithm

AP의 동작은 Affinity Propagation Algorithm Explained에 자세하게 나와 있습니다. 이 글을 계속 읽기 전에 먼저 보시기를 권합니다.

AP는 기본적으로 1개의 Similarity Matrix를 계산하고, 이를 기반으로 Responsibility Matrix와 Availability Matrix를 번갈아 가면서 반복적으로 계산하는데, 수렴상태나 사전에 지정한 반복 횟수에 도달하면 실행을 종료합니다.

먼저, $x_1$ 에서 $x_n$까지의 data point가 있다고 합시다.

Similarity Matrix (s)

Negative squared distance로 두 점 간의 유사도를 나타냅니다. 상수항을 무시하면 gaussian에 log를 씌운 log-probability로도 볼 수 있습니다.

$s(i,k)=-\left|x_{i}-x_{k}\right|^{2}$

Responsiblity Matrix (r)

$r(i,k)$ 는 $k$가 $i$에 얼마나 exemplar로 적합한지를 나타냅니다. (편의를 위해서 $k$는 $x_k$를, i는 $x_i$를 나타냅니다. )

$s(i,k)$는 고정된 값이고, $i$의 exemplar로 가장 적합한 $k’$의 적합도가 높을수록, $k$는 $i$ 에 대한 responsiblity가 낮아집니다.

$i$ 주변에 괜찮은 exempler가 있으면 $k$가 $i$ 에 대해서 부담을 덜 가져도 돼서 $(r,k)$가 음수값을 가지지만, 만일 가장 적합한 $k’$의 적합도가 $s(i,k)$보다 낮다면 $(r,k)$는 양수값을 가질 수 있습니다. 양수라면 $k$가 $i$의 exemplar로, 또한 주변 data point들을 대표하는 cluster center로 선택될 가능성이 커짐을 의미합니다.

$r(i,k) \leftarrow s(i,k) - \max_{k' \neq k} \left{ a(i,k') + s(i,k') \right}$

Availability Matrix (a)

$a(i, k)$ 를 계산할 때는 먼저 $r(i’, k)$에서 양수만을 고려함을 주목해야 합니다. 즉 자신을 제외하고 다른 점 $r’$에 대해서 $r(i’, k)$가 양수가 많은 점 k가 cluster center가 될 가능성이 높습니다. 그만큼 k가 주변의 점들에 responsiblity가 높다는 것이고 그로 인해서 $i$가 보기엔 $k$가 cluster center로서 available 하다고 판단한다고 이해할 수 있습니다.

$a(i,k) \leftarrow \min \left( 0, r(k,k) + \sum_{i' \not\in {i,k}} \max(0, r(i',k)) \right)$

$a(k,k) \leftarrow \sum_{i' \neq k} \max(0, r(i',k))$

sklearn.cluster.AffinityPropagation 구현

sklearn의 AffinityPropagation 구현은 두 가지의 hyperparameter를 제공합니다.

Preference

각 data point들이 얼마다 exemplar로 선택될 가능성이 높은지를 지정하는 것으로, 높은 값을 부여할수록 더 많은 data point들이 exemplar가 되어서 그 결과 작은 클러스터가 더 많이 생기게 됩니다. 반대로 preference가 작을수록, 적은 수의 사이즈가 큰 클러스터가 만들어지는 경향이 있습니다.

Preference는 알고리즘 동작상에서 보면 Similarity Matrix의 대각선 값입니다. 즉 $s(k, k)$ 인 데, 이 값이 $k$가 얼마나 exempler가 선택될 가능성이 큰지 정해주는 것입니다.

Damping factor $\lambda$

Damping factor는 알고리즘의 매 반복마다 Responsiblity Matrix와 Availability Matrix를 업데이트할 때 Exponential weighted average를 적용하는 것입니다. 행렬값을 업데이트할 때 변동성을 줄여주어 그 결과 알고리즘이 noise에 좀 더 robust 해지는 효과가 있으며, 따라서 올바른 damping factor를 지정하면 수렴속도도 더 빨라지고 성능도 더 좋아질 것을 기대할 수 있습니다.

$r_{t+1}(i, k) = \lambda\cdot r_{t}(i, k) + (1-\lambda)\cdot r_{t+1}(i, k)$

$a_{t+1}(i, k) = \lambda\cdot a_{t}(i, k) + (1-\lambda)\cdot a_{t+1}(i, k)$

Examples

먼저, 간단한 데이터에서 k-means와 affinity propagation의 동작을 확인해 봅시다.

import numpy as np
from matplotlib import pyplot as plt
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg', 'pdf')

import seaborn as sns
sns.set()
plt.style.use('ggplot')

from sklearn.datasets import make_blobs
from sklearn.cluster import AffinityPropagation

X, clusters = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
plt.scatter(X[:,0], X[:,1], alpha=0.7, edgecolors='b', cmap=plt.cm.RdYlGn)

ex1_blobs

k-Means는 클러스터 개수(k)를 달리하여 결과를 출력했습니다 . 예상했던 대로, k가 4일 때 가장 좋은 결과를 얻을 수 있습니다.

from sklearn.cluster import KMeans

kmeans_results = []
for k in range(2,8):
    kmeans_results.append(KMeans(n_clusters=k, random_state=0).fit(X))

fig, axs = plt.subplots(2, 3, figsize=(8,5))
axs = axs.flatten()

for i, k in enumerate(range(2,8)):
    ax = axs[i]
    kmeans = kmeans_results[i]
    ax.scatter(X[:,0], X[:,1], c=kmeans.labels_, alpha=0.7, edgecolors='b', cmap=plt.cm.RdYlGn)
    ax.set_title('k = {}'.format(k))
    
plt.suptitle('k-Means Results at different numbers of clusters (k)')
fig.tight_layout()

ex1_kmeans

AP는 damping factor를 기본값 (0.5)로 고정하고, preference를 [-80, 0] 구간에서 변화를 관찰했습니다. Preference가 [-80, -40] 구간에서 가장 좋은 결과를 보여주고, -40 이상부터는 클러스터가 잘게 나누어지는 결과를 볼 수 있습니다.

af_results = []

for pref in range(-80, 1, 10):
    af_results.append(AffinityPropagation(preference=pref, random_state=0).fit(X))
    
fig, axs = plt.subplots(3, 3, figsize=(8, 7))
axs = axs.flatten()

for i, pref in enumerate(range(-80, 1, 10)):
    af_clustering = af_results[i]
    ax = axs[i]
    ax.scatter(X[:,0], X[:,1], c=af_clustering.labels_, alpha=0.7, edgecolors='b', cmap=plt.cm.RdYlGn)
    ax.set_title('Preference = {}'.format(pref))
    
plt.suptitle('Affinity Propagation Results at different preferences')

plt.tight_layout()

ex1_ap

다른 예제도 관찰해 봅시다. 아래의 예제에서는 Preference를 잘 조정해도 깨끗하게 클러스터를 나누지 못합니다. Scikit-learn 문서를 보면 AP를 non-flat geometry에도 사용할 수 있다고 나와 있는데, 잘 안되는 것 같네요. Not-flat geometry라는 건 데이터가 존재하는 부분 공간이 선형이 아닌 굽어져 있는 공간이어서 euclidean distance를 쓸 수 없다고 합니다. 2.3 Clustering

ex2_circles

ex2_ap

마지막 예제로, 데이터의 퍼진 정도가 달라서 클러스터의 크기(공간상의 면적)과 그로 인한 농도가 다를 때의 AP 수행의 결과입니다. Preference를 잘 조정해봐도 클러스터가 깔끔하게 나누어지지 않습니다. 위의 예제와 마찬가지로 scikit-learn 문서에서는 uneven cluster size에 대해서도 사용 가능하다고 나와 있는데, 그렇게 잘 되는 것 같지는 않습니다.

ex3_blobs

ex3_ap

정리

이상으로 Affinity Propagation 클러스터링 알고리즘에 대해서 살펴봤습니다. Scikit-learn 문서에서 k-Means 다음에 소개될 정도로 비중이 있어 보이지만, 자주 쓰일 것 같지는 않습니다. 그 이유로는,

k-Means와는 다르게 k를 지정하지 않아도 된다는 장점이 있지만, 반대급부로 preference를 잘 조정해야 합니다. 그리고 k-Means에서 k를 결정하는 문제는 효과적인 heuristic 한 방법이 있기 때문에 큰 문제가 되지는 않습니다.

이어서, 클러스터의 경계를 나눌 때는 k-Means처럼 centroid 사이의 가운데 지점을 기준으로 나누는 것이 아닌, 각 클러스터의 크기와 주변 점들과의 affinity를 고려해서 클러스터 경계를 나누기 때문에 때에 따라서 더 좋은 결과를 가져올 때가 있지만, 그로 인해 사용하기에 좀 더 어려워집니다.

마지막으로 사실 클러스터링 문제는 data point 간의 distance를, 즉 metric을 어떻게 정의하느냐가 성능을 가장 크게 좌우하기 때문에 좀 더 간단하고 직관적인 알고리즘이 때로는 문제를 풀 때 더 효과적인 것 같습니다.

정리하면, 거의 모든 데이터 문제와 마찬가지로, 알고리즘마다 특성이 있기 때문에 알고리즘이 분석의 목적과 데이터의 특성과 잘 맞으면 좋은 성능을 내겠지요.